Sliderule – the eco-friendly computer from days of old

Some of my favourite computers require no PSU, no batteries, no RAM, no disks, no upgrades and they are 100% resistant to all known malware. No, I’m not talking about some newfangled Linux. I’m talking about good old fashioned sliderules. 🙂

Sliderules top to bottom…

• Top: Darmstadt 304. Despite its German-sounding name, this sliderule was in fact British. 1970’s.
• Middle: Beautifully engineered but rather faded, all-metal (except the cursor) Picket and Eckel N-500-T, from the United states, c/w original real-leather case. Early 1960’s.
• Bottom: The schoolboy’s favourite – a British Thornton AD150 log-log slide rule. This example is a bit battered having also been used for sword fights, whilst waiting for maths class to start. 🙂 Purchased from our school stationery shop in 1974.

A couple of other curios…

• The “Think” block was gift from IBM to my late uncle, who was Head of Data Processing at Esso Refinery, Fawley back in the late 1960’s and early 1970’s. The back is inscribed “Compliments of IBM World Trade Corporation”. “Think” was one of IBM’s advertising slogans, dating right back to the 1920’s. The concept eventually found its way to IBM’s ThinkPad series of laptops in the 1990’s.
• All-metric hard-chromed sprung-steel rule, also from my student days: a British-made Brown and Sharpe – formerly one of the best-known and most influential British machine tool makers, now part of Hexagon AB, a Swedish multinational.

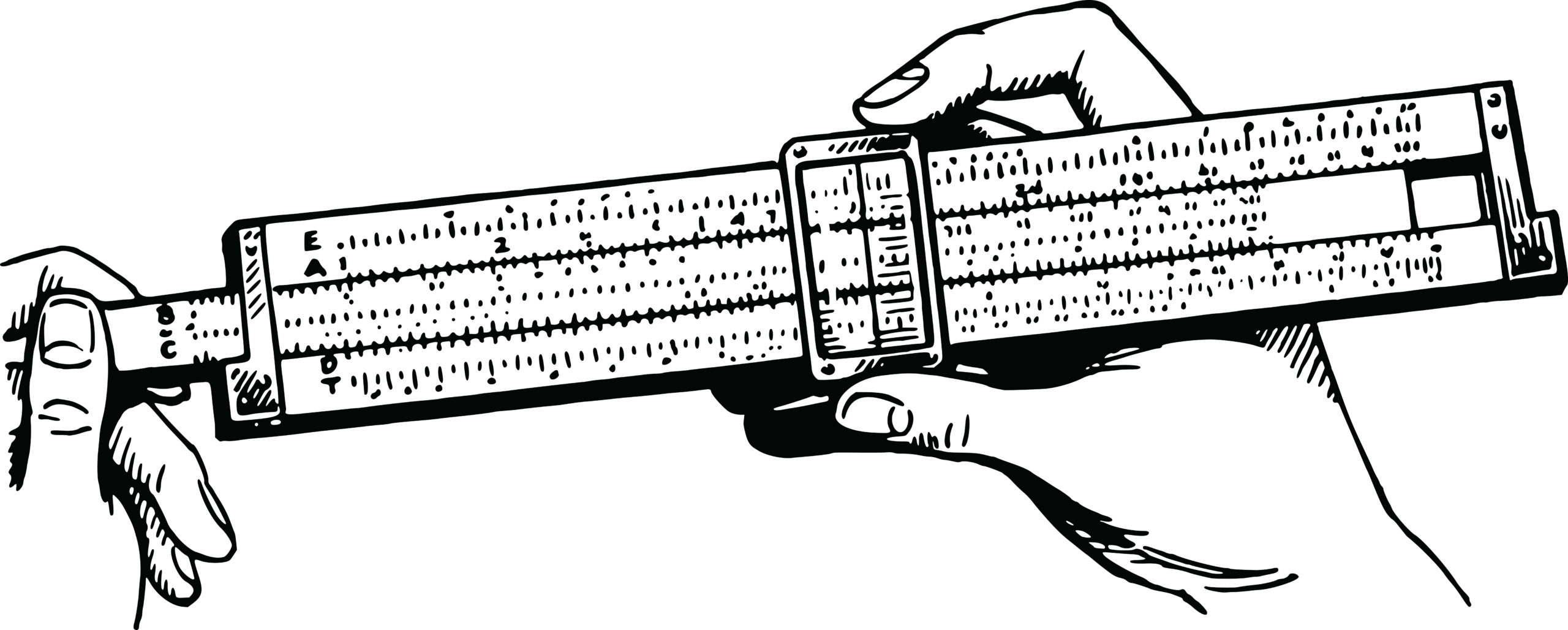
How to use a slide rule

You may remember from your schoolboy or schoolgirl maths, when you add logs, you are multiplying the actual number. Slide rule exploits this. In principle, you have a pair of logarithmic scales that move relative to one another…

In this example, we’ve moved the “C” scale so that its value “1” is directly above the “D” scale value of “2”. I.e. 1×2 =2

As you look along the “C” scale you see that 2×2=4, and further along, 3×2=6 and so on, effectively giving you a graphical two-times-table. If you place “C” scale value “1” over some other “D” value, say 1.2, it will now give you a 1.2 (or 12) times-table. You use the cursor to ensure you have aligned the numbers accurately.

If you run out of numbers on the “C” scale, then align the “1” value on the other end of  the “C” scale, with your chosen value on the “D” scale, thus…

That basically is it! 🙂